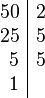imagenes para hi5

Potencias y raíz cuadrada

Con estos ejercicios aprenderás a trabajar con potencias y comprenderás el concepto de raiz y a resolverlas

PRÁCTICA 1



PRÁCTICA 2

PRÁCTICA 3

PRÁCTICA 4 : NOTACIÓN CIENTÍFICA

juego: cuadrado y cubo

PRÁCTICA 5

Una potencia es una forma abreviada de escribir un producto formado por varios factores iguales.
6 · 6 · 6 · 6 · 6 =  6⁵
Base de una potencia
La base de una potencia es el número que multiplicamos por sí mismo, en este caso el 6.

Exponente de una potencia

El exponente de una potencia indica el número de veces que multiplicamos la base, en el ejemplo es el 5.


Una potencia consta de dos partes, por un lado está la base que es el número que se multiplica por sí mismo y por otro el exponente que nos indica el número de veces que se multiplica el número.

Propiedades de la potencias de números naturales
Un número elevado a 0 es igual a 1.
a⁰ = 1
5⁰ = 1
Un número elevado a 1 es igual a sí mismo.
a¹ = a
5¹ = 5
Producto de potencias con la misma base:
Es otra potencia con la misma base y cuyo exponente es la suma de los exponentes.
a^m · a ⁿ = a^m+n
2⁵ · 2² = 2⁵⁺² = 2⁷
División de potencias con la misma base:
Es otra potencia con la misma base y cuyo exponente es la diferencia de los exponentes.
a^m : a ⁿ = a^{m - n}
2⁵ : 2² = 2^{5 - 2} = 2³

¿Cómo se halla el máximo común divisor (m.c.d.)?

Tomamos todos los factores comunes elevados a los menores exponentes











Ejemplo:




Factores comunes (a todos los números): , y elvado al menor exponente (dentro de un recuadro) sería: .
Por tanto:

Cuadrados y cubos

Mínimo Común Múltiplo (m.c.m.)

Mínimo Común Múltiplo (m.c.m.)
El mínimo común múltiplo (m. c. m.) de dos o más números es el menor múltiplo común distinto de cero.
Ejemplo: m.c.m. (10 y 20)=
20:       20 ,40, 60, 80....
10:       10, 20, 30, 40...

m.c.m (10, 20) = 20 es el múltiplo menor que es común a ambos números.
Multiplos: los múltiplos de un número se obtienen multiplicando dicho número por los números naturales 0, 1, 2, 3, 4, 5…..
Ejemplo: múltiplos del 7 son:
7×0=0; 7×1=7; 7×2=14; 7×3=21; 7×4=28; 7×5=35 ….
Tambien se puede calcular el m.c.m mediante la descomposición en producto de factores primos
Ejemplo:
Calcular el m. c. m. (72, 50)
1º Se hace la descomposición de factores siguiendo las reglas de divisibilidad.

 

 

 

Se escogen los factores comunes y no comunes con el mayor exponente y se multiplican.
m.c.m (72 y 50) =           =1800

CRITERIOS DE DIVISIBILIDAD

Antes de empezar te deberías saber las reglas de divisibilidad. Para ello, pulsa sobre la foto.

Mata-mata de números primos y multiplos de 3, 4 ó 6.



Números primos:





Para los alumnos de Apoyo de 5º
Tabla de Multiplicar Pincha Aquí

Tema 2: Operaciones con números decimales

Lectura de números decimales
Escritura de números decimales
Comparación de números decimales
Descomposición de números decimales
Actividades del tema para imprimir

Multiplicación por la unidad seguida de ceros

División por la unidad seguida de ceros

Test de comprobación:Multiplicación de un número decimal por la unidad seguida de ceros
Demuestra que sabes multiplicar y dividir por la unidad seguida de ceros

La recta numérica

Matemáticas interactivas

Se repasan todas las matemáticas. El sitio está organizado por bloques de contenido.

¡¡Bienvenidos al nuevo curso 2011-2012!!
Para comenzar lo haremos REPASANDO los conocimientos  del curso anterior ( nos servirán para hacer la prueba Inicial de curso).

PRUEBA DE EVALUACIÓN INICIAL

ÁREA DE MATEMATICAS. 6º CURSO. ED. PRIMARIA

 

1.- LECTURA Y ESCRITURA DE NÚMEROS NATURALES.

q  Completa con cifras o letras según corresponda:

870.400: _____________________________________________________

Ochenta y tres mil cuatrocientos dieciséis: __________________________

Setenta y nueve mil novecientos noventa:____________________________

24.725.348:____________________________________________________

218.499:______________________________________________________

Doce millones ciento veintiséis mil doscientos cuatro.:__________________

2.- VALOR DE POSICIÓN DE NÚMEROS NATURALES:

q  Observa este número y contesta:

C Millón	D Millón	U. Millón	CN	DM	UM	C	D	U
-	4	8	3	2	9	7	0	5

¿Cuál es la cifra de las centenas?___________________________

¿Cuántas unidades vale la cifra de las centenas? _______________

¿Cuál es la cifra de la unidad de millón?_____________________

¿Cuántas unidades vale la cifra de la unidad de millón?_________

q  ¿Cuál es el valor de posición de la cifra 5 en el número  8 4 5 7 0 ?

_________________________________________________________

q  El número de un billete de lotería en el  4 5 6 7 2.

¿Cuál es la cifra de las centenas? ________________

¿Cuántas unidades vale? _______________________

¿Cuántas unidades vale la cifra 5 ?: _______________

3.- SERIES CON NÚMEROS NATURALES Y DECIMALES.

q  Completa estas series de números naturales:

10.500

11.000

12.000

340.600

540.600

940.600

q  Escribe los números que faltan en estas series:

0’7

0’9

1’9

1’75

1’50

0’5

4.- LECTURA Y ESCRITURA DE NÚMEROS DECIMALES.

q  Completa:

4 unidades 3 décimas 7 centésimas  =     4’37   centésimas

5 décimas 6 centésimas                       =      ____   centésimas

 

6 unidades 8 décimas                         =      ____   centésimas

1 unidad 5 centésimas                        =     ____   centésimas

7 unidades 2 décimas 1 centésima     =     _____  centésimas

q  Completa según ejemplo:

2’158  =  2 unidades, 1 décima, 5 centésimas, 8 milésimas

0’416  =  _______________________________________

0’075  =  _______________________________________

0’003  =  _______________________________________

5.- VALOR DE POSICIÓN EN NÚMEROS DECIMALES.

q  Completa los siguientes cuadros:

D	U	d	c
	3	,2	7

      3 unidades 2 décimas 7 centésimas

	0	,5

                                   _____________________________________________

                       

6	7	,4	8

                                   _____________________________________________

                                  

	3	,1	5

                                   _____________________________________________

6.- COMPARACIÓN DE NÚMEROS DECIMALES.

Observa la siguiente tabla

13’35	13’63	13’62	14’05	14’50
0’235	0’325	0’523	0’532	0’352
1’2	1’3	1’2	1’4	1’6

q  Ordena de mayor a menor cada serie horizontal

7.- LECTURA Y ESCRITURA DE FRACCIONES.

q  Escribe la fracción que tiene por denominador 9 y por numerador 6.

q  Escribe con cifras:

- seis novenos:___________                   doce quinceavos:____________

- cuatro sextos:___________                  dos quintos :________________

- cuatro veinteavos: _______                  tres cuartos:________________

q  Escribe cómo se leen estas fracciones:

_3_ ________________________          _2_: _____________________

  5                                                               6

_6_  ___________________________   _8_: _____________________

 18                                                            12

_7_  _________________________       _15_: ____________________

 12                                                              20

8.- REPRESENTACIÓN GRÁFICA DE FRACCIONES.

q  Colorea en cada figura la fracción que se indica:

                                   _2_

                                     3

                                   _1_

                                     4

                                   _4_

                                     6

q  Representa gráficamente las siguientes fracciones

_3_                                   _2_                             _6_

  6                                       5                                 8

9.- FRACCIÓN DE UNA CANTIDAD.

q  Completa la tabla:

	120	150	300	900
1/2 de
1/3 de

10:- COMPARACIÓN DE FRACCIONES.

q  Escribe el signo >  o < entre cada fracción. Ayúdate coloreando cada fracción:

                                                           _4_              _6_

                                                             7                  7

q  Rodea en cada de pareja de fracciones  la fracción mayor:

a)  _2_  y  _4_                  b) _9_  y _11_                            c)   _4_  y _4_

       5          5                          7          7                            5         7

11.- FRACCIONES EQUIVALENTES.

q  Completa las fracciones equivalentes que se indican:

 2_  =  ___                  _3_ = ___                   _9_ =  ___ = ____

 3          9                      9         3                       9         3         2

 _2_  =  ____              _2_  =   ___                _3_  =  ____ =  ____

   3           12                 6            3                    3           6           9

12.- NUMERACIÓN ROMANA.

q  Indica los valores de los siguientes números romanos

I              V         X         L         C         D         M

                        _1__        ____    ____   ____    ____                ____    ____

q  Completa:

CXXV = _______           216 = _______           XLIX = ______

  715    = _______                        CDL = ______          1.997 = _______

13.- SUMA CON NÚMEROS DECIMALES.

q  Coloca y realiza estas sumas:

2’36 + 1’34 = _______                            23’54 + 32’15 + 0’5 =  _______

479’647  +  563’8  = _________

14.- RESTA CON NÚMEROS DECIMALES

q  Coloca y realiza estas restas:

47’35  –­­  42'735  =                               12’04  – 4’13  =

9’56  – 1’83 =                                    14 –  0’275 =

15.- SUMA Y RESTA DE FRACCIONES DE IGUAL DENOMINADOR.

q  Calcular:

_4_ +_2_  =                     _3_  + _5_   –  _4_  =

  8       8                              9         9           9

_6_  –  _3_  =                               ____ – _3_ = _2_

  7          7                                                    6        6

16.- MULTIPLICACIÓN DE UN NÚMERO DECIMAL POR UN NÚMERO NATURAL.

q  Multiplica:

46’7 x 5   =                                              346 x 2’8  =

17.- MULTIPLICACIÓN DE NÚMEROS DE VARIAS CIFRAS

q  Realiza estas multiplicaciones:

3642  x  254  =                                        261  x  245  =

5031  x  205  =

18.- OPERACIONES COMBINADAS

q  Resuelve estas operaciones:

5 x (10 + 2 – 5)  =                                    3 x (6 – 4 + 1) + 4  =

(2 x 6 ) : 4  =                                            2 + 4 x 3 =

2 x ( _2 _  +  _4_ ) =

          3           3

19.- LA DIVISIÓN.

q  Resuelve las divisiones siguientes:

900 : 25 =                                                            5080 : 8 =

19712 : 352 =                                                                             

20.- RESOLUCIÓN DE PROBLEMAS.

Problema nº 1.- Plantea y resuelve.

            En la tienda librería había 2450 cuadernos. Al inicio del curso se han vendido 170 paquetes de doce cuadernos cada uno.

¿Cuántos cuadernos han quedado sin vender?

Problema nº 2.- Plantea y resuelve.

            Una envasadora se encarga de llenar garrafas de 25 litros.

¿Cuántas garrafas podrá llenar con 1467 litros que le quedan

Problema nº 3.- Plantea y resuelve.

            En un almacén hay 133 cajas con juegos de mesa. Cada caja contiene 25 juegos. ¿Cuántos juegos hay en total?

Problema nº 4.- Plantea y resuelve.

            ¿Cuántos botes con nueve pinturas podemos llenar con veintisiete pinturas?

21.- MEDIDAS DE LONGITUD, CAPACIDAD Y PESO.

q  Completa lo que falta:

2’95  kg. = ___________ g. = _____________dg. =  _______________cg.

     1750  g. = _________________ kg.

   

     23 g. ______________________mg.

q  Expresa estas longitudes en la unidad en que se indica en cada caso:

5 hm = ____________ m             6 dam = ________________ m

15 m = ____________ hm           27 dm = ________________ mm

17 m = ____________ dm          2 km = _________________ mm

q  Completa lo que falta:

12 kl = ________ l = ________ dl = _________ cl = ________ml

36 hl = ______________ dal                  320 cl = ____________ l

22.- MEDIDAS DE SUPERFICIE.

q  Completa la siguiente definición:

“ La superficie que ocupa un cuadrado de un metro de lado es un… ____________________________

q  Nombra tres unidades de superficie más pequeñas que el m²

q  Expresa en cm² las siguientes medidas:

   3 m² =

25 dm² =

q  ¿ Nombra al menos dos múltiplos del metro cuadrado?

23.- EXPRESIONES COMPLEJAS E INCOMPLEJAS.  OPERACIONES.

q  Transforma en incomplejos de gramos y de litros:

3  kg  6 dag   = ___________________________________________

5 hl  62 dl     = ______________________________________________

q  Convierte estas medidas en complejas:

274 m = ______________________________________________________

7.368 mg = ____________________________________________________

24.- MEDIDA DEL TIEMPO.

q  Calcular:

¿Cuántos segundos hay en 15 minutos? _____________________________

¿Cuántos minutos hay en un día? __________________________________

¿Cuántos minutos son dos horas y media? ___________________________

¿Cuántas horas son 3600 segundos? ________________________________

q  Expresa de forma compleja estas cantidades de tiempo:

1 día = _______________________________________________________

25.-  MEDIATRIZ Y BISECTRIZ

q  Dibuja un segmento de 7 cm. de longitud.

Traza su mediatriz

¿Cuánto mide cada una de las partes en que ha quedado dividido el segmento? _____________

q  ¿Qué  clase de ángulo es uno de 75º ?:

Con ayuda de el transportador dibuja un ángulo de 50º:

Traza su bisectriz con ayuda de un compás de un ángulo

26.- FORMAS PLANAS.

q  Dibuja una circunferencia y escribe sus  los elementos.

                                                                      

                                                                                             

                                                                                 

    

q  Construye un hexágono o pentágono, a mano alzada, lo más regular posible.

Traza todas sus diagonales.   ¿Cuántas has trazado? _____________

q  Dibuja estas clases de triángulos: escaleno, equilátero, isósceles

            ________________               ______________               _________________

q  Dibuja triángulossegún sus lados ( acutángulo, rectángulo, obtusángulo)

            _____________                           ______________             _____________

q  Dibuja un cuadrado y un rectángulo. ¿En qué se parecen y en qué se diferencian?

Semejanzas:

________________________________________________________________________________________________________________________________

________________________________________________________________

Diferencias:______________________________________________________

________________________________________________________________

27.- ÁREAS Y PERÍMETROS DE FORMAS PLANAS.

q  El perímetro de un triángulo equilátero mide 18 cm. ¿Cuánto mide su lado?

_____________________________________________________________

q  El perímetro de un rectángulo es de 8 dm. Uno de sus lados mide 1dm. ¿Cuánto miden los demás lados?

_____________________________________________________________

q  Calcula el área de los siguientes polígonos:

Un cuadrado de 6 cm de lado: ____________________________________

Un rectángulo de 9 cm de base y 4 cm de altura._______________________

Un triángulo de 4 cm de base y 12 cm de altura. _______________________

28.- POLIEDROS Y CUERPOS REDONDOS.

q  Marca con una X  la afirmación correcta:

	Prisma	Pirámide	Cilindro	Cono
Tiene una base		X		X
Tiene dos bases
La base (o bases) es un polígono
La base (o bases) es un círculo
Las caras laterales son rectángulos
Las caras laterales son triángulos

29.- MODA Y MEDIA ESTADÍSTICA.

q  En el ejercicio anterior, ¿cuál es el valor que representa la moda?

q  Calcula la edad media de estas personas:

Luis 50 años         Ana: 24 años        Reyes: 30 años           Mikel: 20 años

Suma de las edades: _____ + ______ + _______ + ________ = __________

Número de personas: ________

Media de edad:_______ : ________ = _________

30.- AZAR Y PROBABILIDAD.

q  En una caja hay 10 bolas, todas de colores distintos.

¿Es seguro que….?

- ¿….al sacar dos, éstas serán de distinto color? _____________________

- ¿…al sacar una, ésta será de color rojo?: __________________________

- ¿…al sacar tres, la tercera será negro?: ___________________________

q  En la lista de clase figuran, por orden alfabético, 14 niñas y 11 niños.

¿Es seguro que los cinco primeros de la lista son chicos? ______________